Deterministisches Chaos

Chaos. Das erhalte ich, wenn ich den unterschiedlichen Punkten eines Bildes zufällige Farbwerte zuweise. Oder wenn ich mir die Verteilung von Sandkörnern in einer Strömung ansehe oder Staub im Wind. Wenn ich Popcorn mache, welches Korn poppt als nächstes und fliegt wohin? Oder Mikadostäbe auf den Tisch werfe. Wenn ich eine handvoll Getreide in eine Hühnerschar schleudere. Oder wenn die Potse gestürmt wird.

Eine grobe Idee vom Chaos ist wohl, das man es in unberechenbaren Systemen findet; in Mengen, über deren Einzelemente sich keine Aussage über Ort, Geschwindigkeit, Temperatur, Farbe, Verhalten oder so treffen lässt. Aber dass es Systeme mit berechenbarem, mit deterministischem Chaos gibt, war mir lange nicht klar. Als ich auf die logistische Gleichung gestoßen bin, war das wie eine kleine Offenbarung, denn in ihrem Licht erscheint der Übergang von deterministischen zu chaotischen Systemen plötzlich ganz klar und verständlich. Von der Idee her kannte ich das Prinzip eigentlich schon von Hashing-Funktionen, die ja versuchen einen Wert auf einen anderen Wert möglichst chaotisch, also nicht rückberechenbar, abzubilden: Pseudo-Chaos, das ja trotzdem irgendwie in einem deterministischen Computer berechnet werden muss.

Aber die logistische Gleichung offenbart eine Schönheit, die ich bei Hashing-Funktionen bisher nicht entdeckt habe.

Zunächst ist sie so definiert:

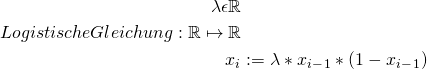
Das λ lässt sich als Wachstumsfaktor eines dynamischen Systems auffassen, die einzelnen x_i als die Systemwerte zum Zeitpunkt i. Für x0, den Startwert des Systems, kann meines Wissens irgendeine positive reele Zahl genommen werden – zumindest hat das bei mir immer geklappt. 0,2 geht gut, aber auch mit allen anderen Startwerten pendelt sich die Folge schon bald bei endlich vielen Häufungspunkten ein. Und da sind wir schon beim Knackpunkt: die Folge hat Häufungspunkte und diese lassen sich plotten.

Mich erinnert die Folge immer stark eine eine verfeinerte Form der Fibonacci-Folge, mit konfigurierbarem Wachstums- bzw. Sterbefaktor.

Das war mein erster Plot der Funktion, und auch mein zweiter, dritter, vierter und zwanzig spätere sahen so ähnlich aus: viele unabhängige, sich überlagernde Wellen. Der abgebildete Wertebereich liegt übrigens zwischen 0 und 1. Da ich das ganze in Javascript schreibe und dachte, dass dies nur mal ein kleines Coding-Experiment für einen Abend wird, habe ich auch kein Mathe-Framework genommen, sondern alles direkt mit vanilla-Javascript auf einer HTML-Canvas gerendert.

Auch wenn in diesem Diagramm nicht das »Große Ganze« dargestellt wird, finde ich es schon faszinierend, dass hier offenbar irgendwelche periodischen, wellenförmigen Kurven erkennbar sind.

Leicht frustriert habe ich das ganze erstmal liegen lassen, aber da mich das Problem nicht in Ruhe gelassen hat (hey, das haben Leute vor 40 Jahren schon mit ihren Taschenrechnern hinbekommen), wollte ich es doch nochmal wissen, und habe die Render-Routine etwas ausgebaut.

Irgendwann habe ich meine Gewichtungsfunktion etwas geändert: je nachdem, wie häufig ein Häufungspunkt in der Folge auftaucht, bekommt er eine Gewichtung. Häufige Häufungspunkte werden stärker gezeichnet, seltene werden schwächer gezeichnet (eigentlich tauchen alle Häufungspunkte unendlich oft auf, aber meine Iterationstiefe ist ja endlich). Außerdem habe den Bildausschnitt angepasst und plötzlich bekam ich das hier. Yeah!

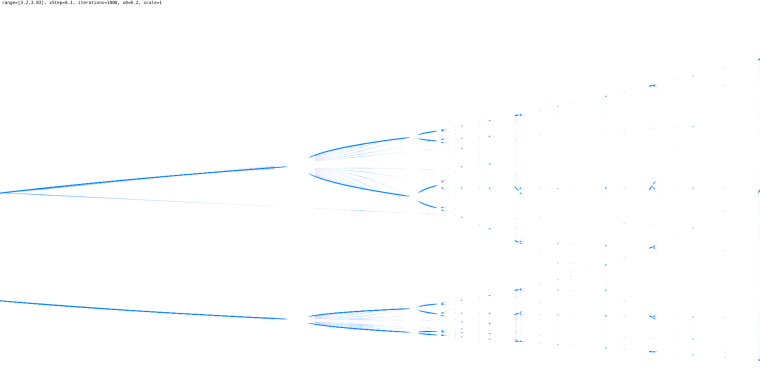
Schon ziemlich nah dran, oder?

Jedenfalls war ich äußerst irritiert wegen der vielen 'Artefakte', besonders wegen der Häufungspunkte, die viele weitere Linien und Wellenmuster bildeten, die ich anhand der vorher gesehenen Plots bei Wikipedia und diverser Mathe-Foren nicht erwartet hatte. Da wurde mir erst klar, dass ich an meinem Häufungspunkt-Kriterium noch etwas arbeiten musste, also habe ich noch einen Schwellwert eingefügt: Häufungspunkte unter 5% des Gesamtanteils werden nun gar nicht mehr geplottet. So versuchte ich, den feinen 'Artefaktstaub', dessen Struktur die endliche Iterationstiefe nicht erfassen kann, auszublenden.

Und so kam diese Bild zum Vorschein, das ich schon die ganze Zeit erwartet hatte: ein wunderschöner Plot, reich an Gabelungen und Detail dazwischen. Die Zweige, um die sich die Häufungspunkte sammelten (ich hatte ein Epsilon von 10^(-10) verwendet) waren noch deutlich vielfältiger an Details, als ich es erwartet hatte.

Hier der schönste Plot bisher (Stand Dezember 2018):

Von links nach rechts, also mit wachsendem Lambda, wächst die Zahl der Häufungspunkte zwischen den Hauptäsen; man spricht von einer Periodenverdopplung, und interessanterweise ist das Verhältnis zweier beliebiger aufeinanderfolgenden Periodenlängen Konstant (erste Feigenbaumkonstate δ=4,669...), das Verhältnis der Gabelungsbreiten ebenso (zweite Feigenbaumkonstante α=2,502...).

Und hier ist auch das Auftreten des deterministischen Chaos zu erkennen: es wird eine immer höhere Iterationstiefe und eine immer feinere Aufteilung der λ-Achse benötigt, um überhaupt nachvollziehbare Häufungspunkte zu finden, da die schiere Zahl der Häufungspunkte immens zunimmt.

Und dennoch ist jeder Häufungspunkt mit ausreichender hoher Iterationstiefe berechenbar, lediglich die Abweichung zwischen naheliegenden Lambdas wird immer unvorhersehbarer: der Übergang von einer deterministischen Funktion zum Chaos.

Den obigen Plot im Bereich [3.2...3.83] gibt es als Grafik mit 13776x9024 Pixeln und

• 500 Iterationen für jedes Lambda
• 10 Berechungen pro Pixel (λ-Schritt: 0.1)
• sichtbar ist der Bildbereich [0,1]
• der Startwert x0 ist hier 0.2

screenshot-feigenbaum-2018-12-12-4-x8.png (40 MB)

Anfangs dachte ich ja, die Feigenbaum-Bifurkationen seien 'echte' Bifurkationen, also Binärbäume mit Verzweigungen von jeweils zwei Ästen, und dass der Raum dazwischen leer wäre. In Wirklichkeit passiert hier noch viel mehr.

Spannend ist auch der 'fast lineare' Ast, der gleich nach der ersten Gabelung bei ~λ=0 zu sehen ist und sich lange Zeit fast linear fortsetzt:

[Bild von der ersten Gabelung]

Eine Live-Demo für den Browser gibt es hier: https://www.int2byte.de/public/feigenbaum-plot/main-feigenbaum.html

Und den Quellecode gibt es hier: https://github.com/IkarosKappler/feigenbaum-plot

(Außerdem ist eine plot-boilerplate.js entstanden, die alle bei der Programmierung gesammelten Plot-Funktionen bündelt.)

Da an den Verzweigungspunkten viele spannende Dinge passieren, hier noch ein paar weitere Plots:

Anmerkung zum ersten Absatz: Ich fand die Poste selbst nie chaotisch. Es war ein fester Ort schöner, künstlerischer, freier Subkultur, ein Ort des Experimentierens und des Sich-Begegnens mit liebevollen Menschen.