Truchet-Kachelungen

Truchet-Kachelungen

oder diese Muster mit den Würmern.

Irgendwann um 1700 stellte wohl mal jemand fest, dass mit quatratischen Keramik-Kacheln interessante kontrastreiche Muster erzeugt werden können, indem die Kacheln einfach diagonal geteilt und weiß-schwarz bemalt werden.

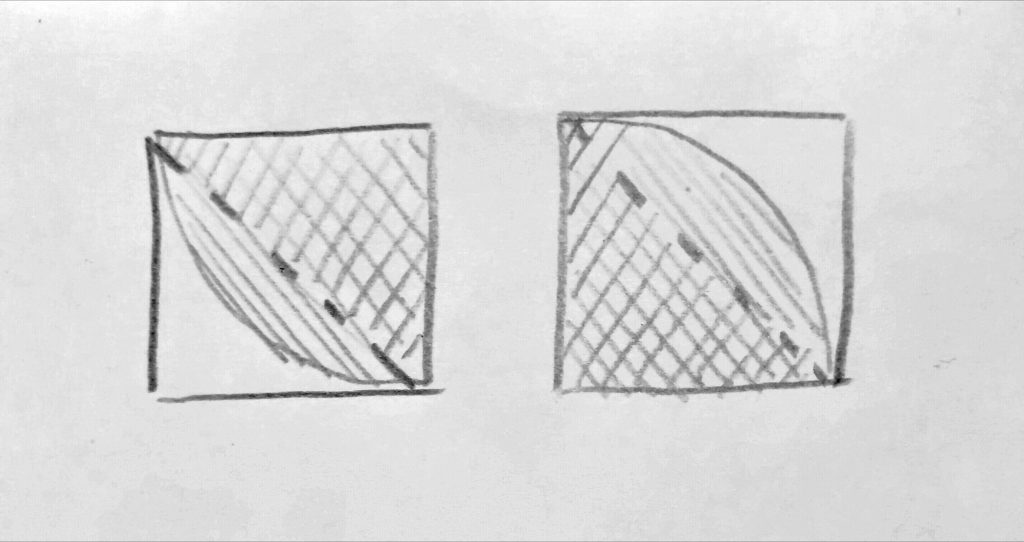
Ihr merkt bestimmt schon, dass es sich hier um dieselbe Kachel handelt, die um 180° gedreht wurde. So wird es im Folgenden noch mit vielen Kacheln geschehen. In moderneren Varianten können wir häufiger die Version mit ¼Kreisbögen finden, und oft sind auch schon 2×2 Kacheln zu einer neuen Kachel zusammengefasst:

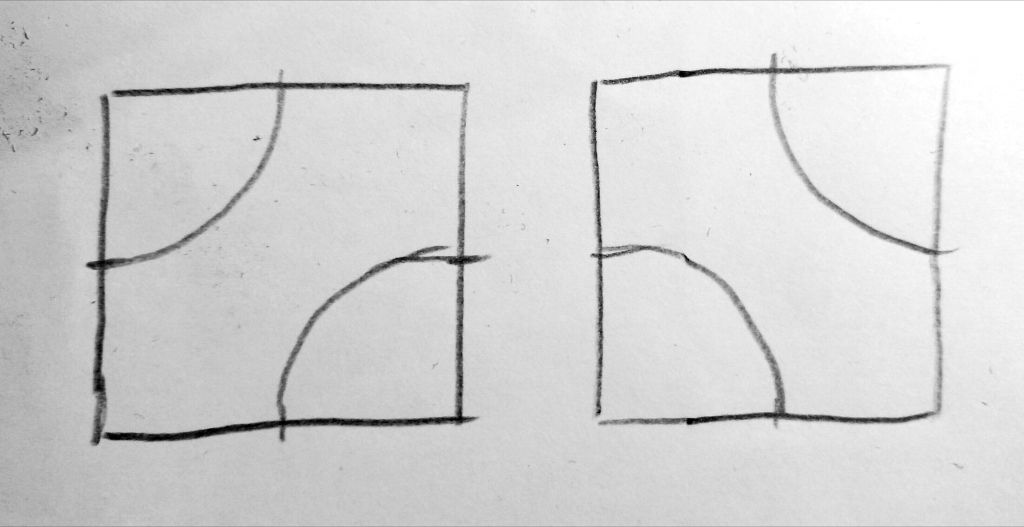
Füllen wir eine Fläche damit. Jede Kachel bekommt eine zufällig gewählte Drehung.
So ergibt sich ein Muster:

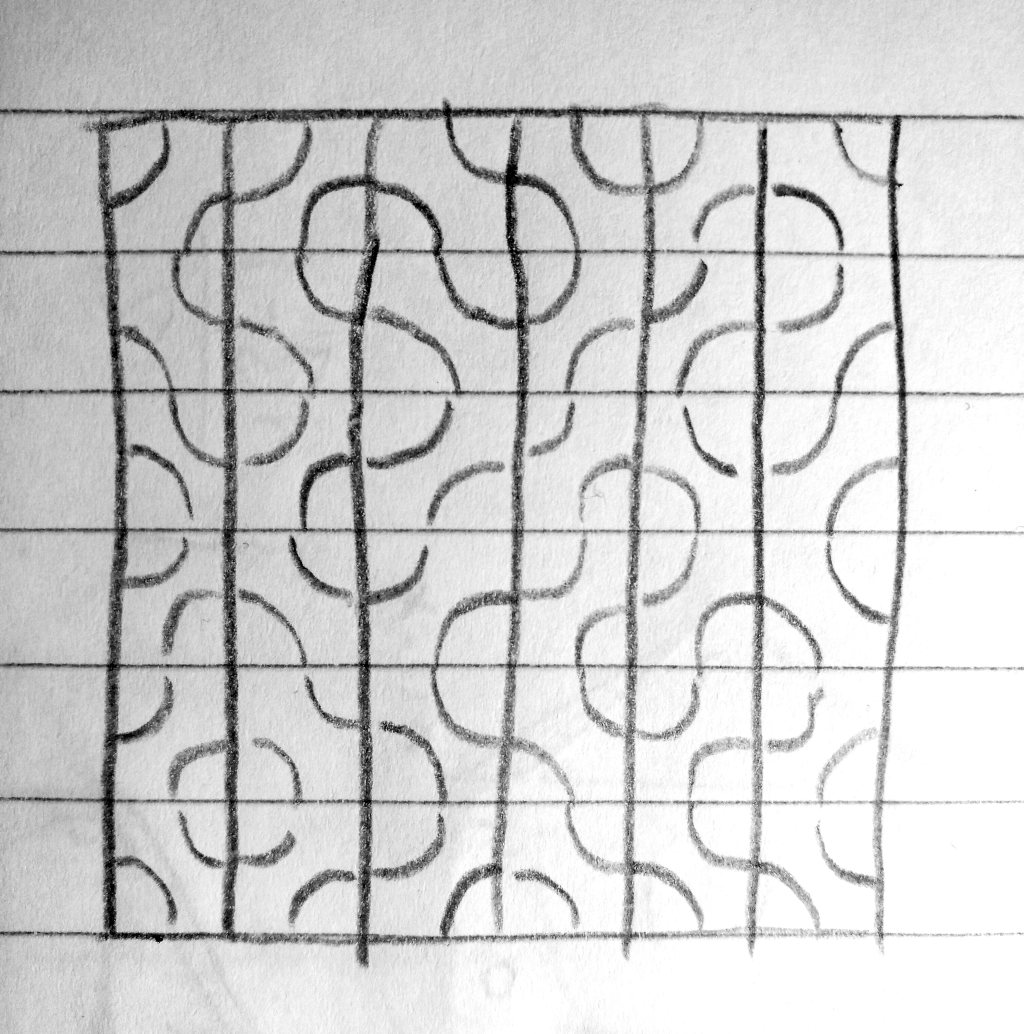
Immer wieder finden sich im Internet diese wurbeligen Füllmuster, die irgendwie aus Kreisen und Kurven bestehen, aber doch in eine darunter liegende klare Geometrie passen: Truchet-Kachelungen.

Dabei handelt es sich primär nicht um eigenständige Kachelungen. Es sind Muster innerhalb vorgegebener Kachelungen der 2D-Ebene, die so konstruiert sind, dass sie an den Kachelkanten genau aneinander passen. Solange alle Kantenlängen der Grundkacheln gleich sind, sind sie leicht zu erzeugen.

Die Idee ist: jede Kachelkante wird in n Segmente zerteilt (z.B. n=1, n=2 oder n=3). Die dabei entstehenden Punkte auf den Kachelkanten bilden die Verbindugsstücke für Pfade, die durch die Kacheln laufen sollen. Der erste Schritt von n=1 zu n=2 ist eben schon automatisch geschehen, indem wie zwei elementare quadratische Truchet-Kacheln zu einer neuen 2×2-Kachel zusammengefasst haben.

Es ist ein wenig wie bei Girih-Mustern: wir nehmen eine vorhandene Kachelung und malen Linien darauf. Jede Kachelkante darf dabei nur exakt n mal durchdrungen werden.

Motivation

Warum eigentlich? In den letzten Monaten sind mir häufiger diese "Muster mit den Würmern" (wie eine geliebte Person sie nennt) untergekommen und irgendwann fiel mir auf, dass sie einem festen Muster folgen:

Hier vier Truchet-Kachelungen mit n=1 bzw. n=2 (von @daveyang):

Mein Ziel war nun: ein Programm zu schreiben, das solche Muster erzeugt. Umgesetzt habe ich dies mit plotboilerplate, aber schaut euch auch mal p5js oder d3js an. Dies sind coole Javascript-Libraries für grafische 2D-Umsetzungen.

Definition der Grundkacheln

Die wohl einfachste, leicht zu berechnende und somit naheligende Grundform ist wahrscheinlich das Rechteck bzw. das Quadrat. Wir geben uns also eine Rastergröße z.B. mit `countH` und  `countV` für die horizontale und vertikale Kachelanzahl vor. Hier `countH=5` und `countV=5` und erzeugen uns 5×5 rechteckige Kacheln.

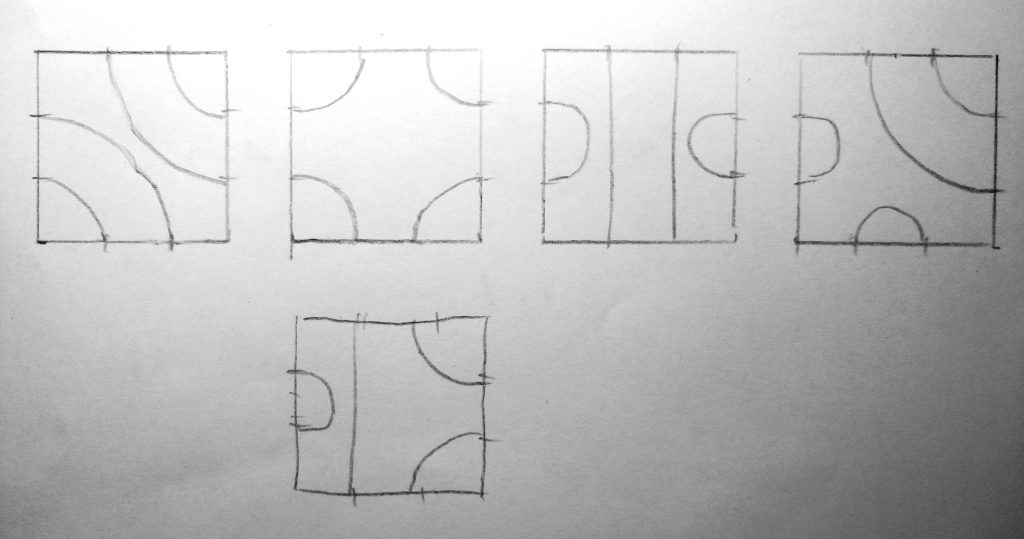
Nun überlege ich, wie viele Pfadpunkte ich auf jeder Kante haben möchte und entscheide mich für `n=2`. Dies habe ich in der Demo fest eincodiert, denn für jede Kachelform und jede Anzahl Pfadknoten ergibt sich eine eigene, feste Grundmenge an möglichen Kachellayouts. In diesem Fall des Quadrats mit `n=2` sind es 5 Möglichkeiten, wie wir oben in der Skizze schon gesehen haben.

Per Zufall wählen wir für jede Kachel ein Muster und eine Ausrichtung und erhalten eine Menge aneinandergrenzender Pfadstücke. Schon ganz schick! Achja: an jeder Kachel-Außenseite füge ich noch ein abschließendes Pfadsegment entsprechend der Kachelregeln hinzu. So erhalten wir schöne geschlossene, zusammenhängende Pfade.

Nun lasse ich einen Pfaderkennungsalgorithmus darüber laufen, der aneinandergrenzende Pfadsegmente zu ganzen, zusammenhängenden Pfaden zusammenfügt. Und voilá, schon haben wir ein Truchet-Muster zu unserer quadratischen Kachelung erhalten. Die Pfade kann man nun auch füllen. Sind ja geschlossen.

Live-Demo: so sieht's aus.

Pfadsegmente: your choice, your fun

Übrigens verwende ich für die einzelnen Pfadsegmente kubische Beziérkurven. Sie sind einfach handzuhaben und generell sehr praktisch für gebogene und geschwungene Formen.

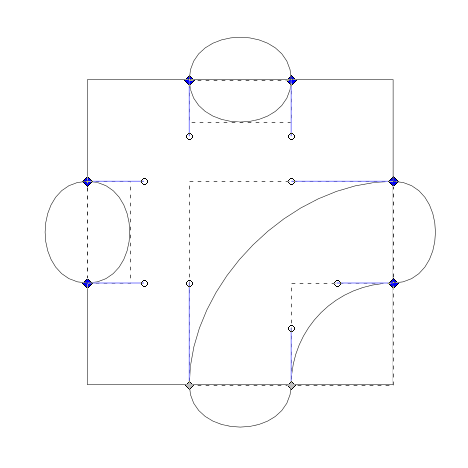
Grundkachel-Variante: Dreieck

Was ist eine andere naheliegende Grundform, mit der sich Flächen füllen lassen?

Das Dreieck.

Die Vorgehensweise ist hier analog zum Quadrat:

• fülle eine Fläche mit Dreiecken
• definiere die Pfadeintrittspunkte auf den Dreieckskanten (hier wieder mit `n=2`)
• verbinde die Pfadpunkte jeder Dreiecks-Kachel mit zufällig generierten Pfaden (überschneidungsfrei natürlich)
• lasse dir zusammenhängende Pfade ermitteln
• zeichne die ermittelten Pfade schön, fülle sie eventuell

Die Pfade definiere ich wieder mittels Beziér-Kurven.

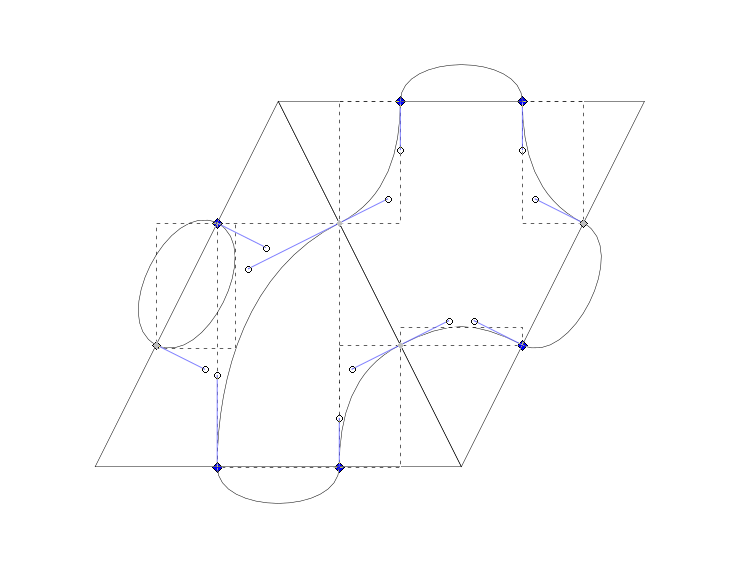
Die dazugehörige Live-Demo findet ihr hier.

Das Ergebnis sieht dann so aus: ähnlich, aber doch anders als bei der quadratischen/rechteckigen Grundkachel.

Variante: Kairo-Kachel

Über die letzten Jahre hat sich eine Kachelform als meine Lieblingskachel herauskristallisiert: die Kairo-Kachel, oder auch p4g der pentagonalen Typ4-Kachelungen.

Wie man mit Sechsecken die Fläche füllt, weiß jede Biene. Aber mit Fünfecken?! Klar, diese gehören nicht zu den platonischen Parkettierungen, weil die Kacheln nicht regelmäßig sind, also unterschiedlich große Innenwinkel haben. Aber cool sind sie schon:

Die Pfadgenerierung zu jeder Kachel sieht dann so aus (wieder mit `n=2`):

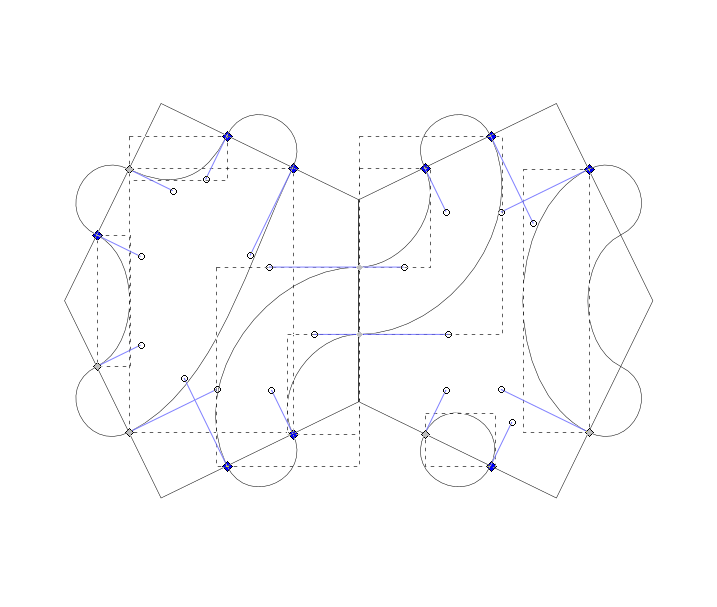
Hier ist auch eine Live-Demo zu finden.

Und das sich daraus ergebende Truchet-Muster so:

Variante: pentagonale p4-Kachelung

Eine andere Variante der pentagonalen P4-Kachelung basiert auf einem quadratischen Grundmuster mit dreieckiger Erweiterung.

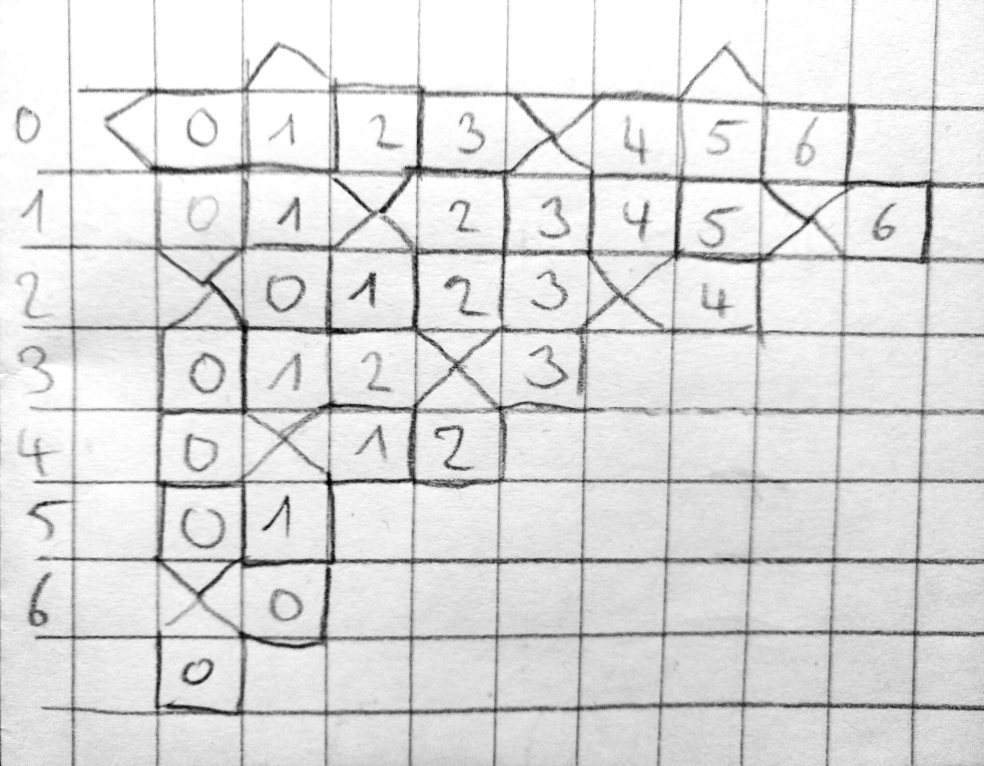
@KaufmanRoni hatte sie auch schon in einem ursprünglichen Post präsentiert, der mir hier als Inspiration diente. Die Basiskachelung heißt auch pentagonalen Typ-4-Kachelung:

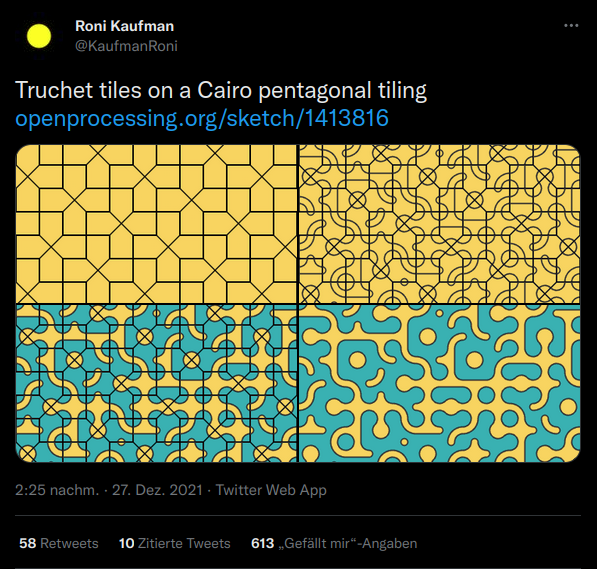
Die 2 bedeutet hier letztlich: auf jeder Kante geht ein Pfad rein und ein Pfad raus.

Ein deutlicher Unterschied ist hier aber leicht sichtbar: die Kantenlänge ist nicht fix, jede Kachel hat drei lange und zwei kurze Kanten. Entsprechend ist die Pfadknoten-Aufteilung hier eine andere mit n={1,2}, je nach Kantenlänge. Lange Kanten haben zwei Knoten, kurze Kanten nur eine. Die Summe der Pfadknoten ist aber 8 und somit eine gerade Anzahl, also lassen sich eingehende und ausgehende Pfade weiterhin nach dem alten Schema erzeugen.

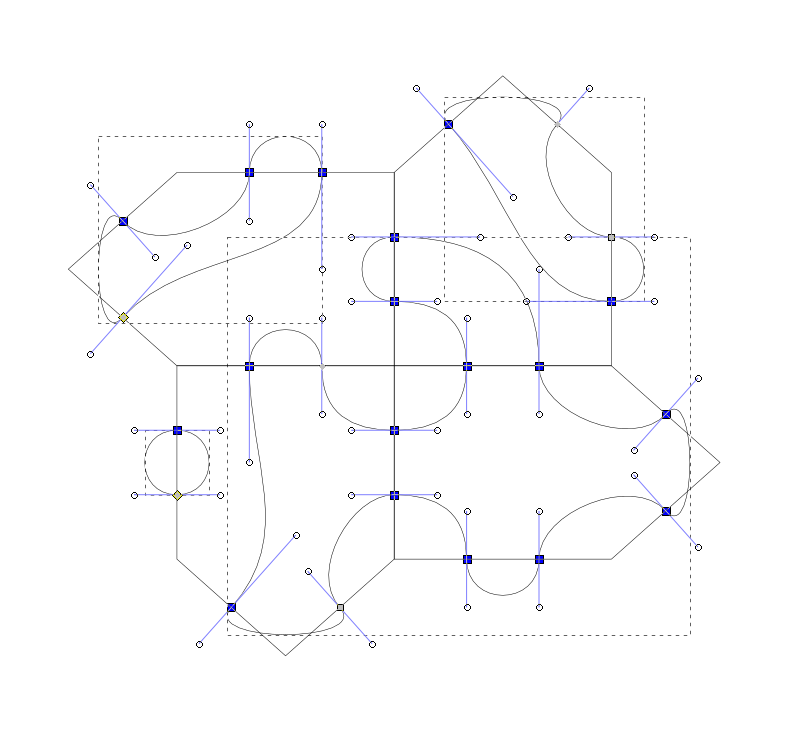
Es gibt natürlich auch eine Live-Demo.

Weitere nicht-einheitliche Kachelungen

Weiterführend können Parkettierungen natürlich auch aus unterschiedlichen Kacheltypen aufgebaut werden, zum Beispiel aus Quadraten + Dreiecken. Mir fallen spontan auch Girihs als mögliche Basiskacheln ein, oder hat schon einmal jemand Penrose-Parkettierungen versucht?

Und was hat Kusamehewa hier getan? Mit n=? und einer nichteinheitlichen Basiskachelung? Kann wer die Konstruktionsschritte erkennen?

Weiter bin ich noch nicht

Aber der nächste kreative Freizeitschub kommt bestimmt. Oder wollt ihr nicht mal wieder etwas programmieren?

Die Codebase hierfür gibt's jedenfalls auf Github.

Joa und irgendwann landen wir dann hier.

Viel Spaß und bleibt bunt, my queer & non-queer, trans and cis, binary & non-binary friends!

Glitches ahoi!

Auf dem Weg zur funktionierenden Truchet-Berechnung können uns viele Coding-, Logik- und Rechenfehler unterlaufen. Fehler müssen aber nicht immer zu hässlichen Ergebnissen führen. Hier seht ihr ein paar Fails aus der Entwicklungsphase. Auch Fehler können Spaß machen ^^