Lightning-Algorithmus

 
Matt Henderson und Brady »Numberphile« Haran haben neulich ein schniekes Video über die Visualisierung des »Breitensuche-Algorithmus« gemacht. Sie nennen es hier »Lightning-Algorithmus«.
 
Nach dem ersten Anschauen war ich so beeindruckt von der Einfachheit und Schönheit der Umsetzung, dass ich sie einfach selbst mit Javascript implementiert habe.
 
Das Script rendert die Einzelschritte, die der Algorithmus bei der Suche nach einem kürzesten Weg in einem Labyrinth durchläft, in einer SVG-Grafik.
 
 
Eine Live-Demo gibt es hier
 
Und den kompletten Quellcode hier
 
Numberphile's Video
 

Eigentlich ist die Breitensuche ein alter Graphen-Suchalgorithmus und eine Variation des Dijkstra-Algorithmus von 1959. Rosetta-Code notiert ihn in ca 30 Zeilen, die Javascript-Variante hat 60 Zeilen. Also echt kurz und schon ziemlich alt für Computerzeitalter-Jahre. Keine besonderen Datenstrukturen sind nötig (außer einem Stapelspeicher/Stack oder einer Warteschlange/Queue zum Speichern der Zwischenschritte) und die Ausführung lässt sich ebenfalls leicht nachvollziehen:

Dijkstra bei RosettaCode

 

Dijkstra-Animation

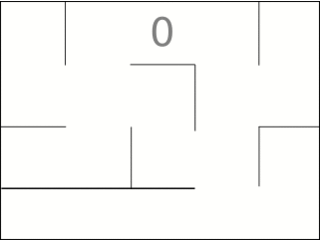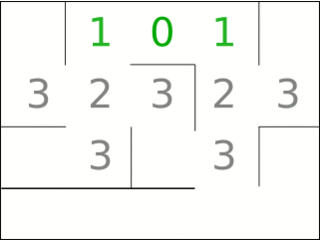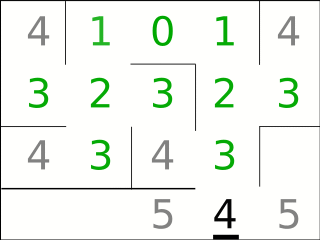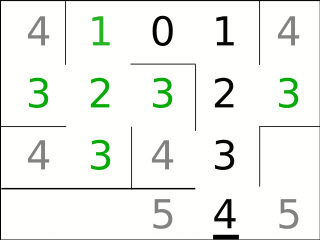
Ob der Dijkstra-Algorithmus eine Breitensuche oder eine Tiefensuche ausführt, hängt vom Puffer-Typ ab, der die Zwischenergebnisse speichert:

  • Eine Warteschlange/Queue liefert eine Breitensuche
  • Ein Stapel/Stack liefert eine Tiefensuche

Desweiteren sind im generierten Labyrinth alle benachbarten Knoten gleich weit voneinander entfernt, d.h. es müssen keine »kleinsten Entfernungen« ermittelt werden. Lediglich lege ich eine bevorzuge Suchrichtung fest: horizontale Nachbarn zuerst, vertikale danach. So läuft die Suchfront zuerst in die Breite, falls das Labyrinth dies zulässt, und erst danach in die Tiefe.

Der Quellcode für einen einzelnen Iterationsschritt:

// +---------------------------------------------------------------------------------
// | Calculates the next step of the BFS: all rectangles on the current frontier
// | checks for non-visited rectangles and marks them to use as the new frontier
// | in the next iteration.
// +-------------------------------
var nextStep = function () {
// Calculate next iteration of the breadth-first-algorithm
stepNumber++;
var newQueue = [];

for (vark = 0; k < queue.length; k++) {
// Find ways that are not blocked
var tuple = queue[k];
var i = tuple.i;
var j = tuple.j;
if (j - 1 >= 0 && !(mazeMatrix[j][i] & BORDER_TOP) && !visited(j - 1, i)) {
// Mark the next reachable entry to the top
solutionMatrix[j - 1][i].step = stepNumber;
solutionMatrix[j - 1][i].predecessor = { j:j, i:i };
newQueue.push({ i:i, j:j - 1 });
config.drawPathTraces && makeTrace(j, i, j - 1, i);
}
if (i - 1 >= 0 && !(mazeMatrix[j][i] & BORDER_LEFT) && !visited(j, i - 1)) {
// Mark the next reachable entry
solutionMatrix[j][i - 1].step = stepNumber;
solutionMatrix[j][i - 1].predecessor = { j:j, i:i };
newQueue.push({ i:i - 1, j:j });
config.drawPathTraces && makeTrace(j, i, j, i - 1);
}
if (i + 1 < mazeMatrix[j].length && !(mazeMatrix[j][i] & BORDER_RIGHT) && !visited(j, i + 1)) {
// Mark the next reachable entry
solutionMatrix[j][i + 1].step = stepNumber;
solutionMatrix[j][i + 1].predecessor = { j:j, i:i };
newQueue.push({ i:i + 1, j:j });
config.drawPathTraces && makeTrace(j, i, j, i + 1);
}
if (j + 1 < mazeMatrix.length && !(mazeMatrix[j][i] & BORDER_BOTTOM) && !visited(j + 1, i)) {
// Mark the next reachable entry
solutionMatrix[j + 1][i].step = stepNumber;
solutionMatrix[j + 1][i].predecessor = { j:j, i:i };
newQueue.push({ i:i, j:j + 1 });
config.drawPathTraces && makeTrace(j, i, j + 1, i);
};

if (j + 1 >= mazeMatrix.length) {
// This will terminate the search algorithm
terminationEntry = { j:j, i:i };
}
}
queue = newQueue;
};

 

Das Labyrinth wird zufällig erzeug aus gegebener Zellenbreite und -Höhe und entsprechenden vertikalen und horizontalen Wandwahrscheinlichkeiten. Die Startpositionen liegen am oberen Rand (eine oder viele oder die ganze Zeile) und streben danach, einen Weg nach unten zu finden. Sobald eine Barriere erreicht wird, weicht der Lösungsweg nach links oder rechts aus (erst links, bei Fehlschlag rechts, per Implementierung) und sucht von dort weiter.

Alle Lösungen werden Schrittweise parallel berechnet und in der Queue für jeden Schritt zwischengespeichert. Sobald ein Weg an das untere Ende des Labyrinths gefunden wurde, endet der Algorithmus und markiert diesen kürzesten Weg, der oft Blitzform hat. Badaboom!

Die Lösung muss nicht eindeutig sein, es kann mehrere geben. Es kann auch keine Lösung geben, wenn das Labyrinth entsprechend kontruiert wurde.

Hier habe ich mal einen Durchlauf als Video aufgenommen:

 

 

 

 

Conway's Game of Life

Klar, wer denkt bei Zellautomaten nicht an »Conway's Game of Life« von 1970? John Conway (schon wieder 'n Typ, sorry) definierte dieses Spiel-ohne-Spielerïnnen mit wenigen einfachen Regeln:

  • eine lebendige Zelle bleibt lebendig, wenn sie zwei oder drei lebendige Nachbars hat
  • sie stirbt (arme Zelle ◕෴◕), sobald sie weniger als zwei lebendige Nachbars hat
  • eine Zelle wird lebendig, sobald sie genau drei lebendige Zellen als Nachbars hat
  • Zellen mit mehr als drei lebendigen Nachbars sterben an Überbevölkerung

Diese Regeln können leicht variieren mit unterschiedlichen Ergebnissen in den Populationsentwicklungen.

Im Wikipediaartikel ist eigentlich schon alles beschrieben und selbst die großartigen Macher_innen von RosettaCode haben schon Implementierungen in vielen unterschiedlichen Sprachen gesammelt.

Das Spiel/der Automat startet mit einer gesetzten Anfangskonfiguration und läuft dann von selbst. Perfekt also, um das ganze mal in Javascript in einem SVG zu rendern. Im Wesentlichen habe ich Teile aus der Lightning-Demo sinnvoll wiederverwendet.

Eine Live-Demo gibt es hier zu sehen: ein sogenannter Glider-Spawner.

Conway's Game of Life

 

Und der Quellcode is hier zu finden.

Als Grundstruktur für ein Biotop wird ein zweidimensionales Array als n×m-Matrix verwendet. Das Biotop selbst kann also nicht wachsen, wenn es einmal angelegt wurde.

 

 

Conway's Game of Life
Conway's Game of Life
Conway's Game of Life

Einfach nur 1:1 Conway zu implementieren wäre etwas lame. Wichtig war mir, das ganze als SVG-Ausgabe zu programmieren (ja, es ist eine animierte SVG-Grafik, die direkt über DOM-Manipulation angepasst wird).

  • Also gab es noch Spuren-der-Lebendigkeit, damit besser ersichtlich ist, wo kürzlich Leben war.
  • Und bunt sollte es sein können, also sind alle Farben frei konfigurierbar (eventuell habe ich bei der Wahl der Standardfarben gerade Daði & Gagnamagnið gehört, aber nur eventuell)

Hier ist mal eine Aufzeichnung meines Lieblings-Formation: das r-Pentomino.

Leiser Start, aber echt wildes Leben.